Understanding Alpha-Beta ($\alpha\beta$) and dq0 Axes in 3-Phase Systems
In electrical engineering, especially with AC machines and power electronics, analyzing three-phase systems can be complex. This is where transformations like Alpha-Beta ($\alpha\beta$) and $dq0$ come in handy.
What are Alpha-Beta ($\alpha\beta$) Axes?
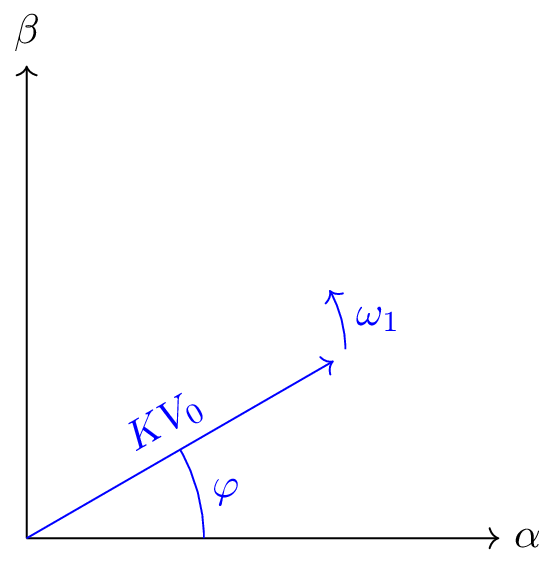
The Alpha-Beta ($\alpha\beta$) axes form a stationary two-axis reference frame. They are the core of the Clarke transformation, which converts three-phase quantities (like voltages or currents) into a simpler, two-dimensional representation.
- The Alpha ($\alpha$) axis is typically aligned with one of the original three-phase axes (e.g., phase 'a').
- The Beta ($\beta$) axis is orthogonal (at 90 degrees) to the alpha axis.
- There's also a zero-sequence (0) component for common-mode or unbalanced parts of the system. For balanced systems, this component is zero.
This transformation simplifies analysis by representing three interdependent AC quantities as two orthogonal components in a stationary plane.
The Clarke Transformation Matrix
The transformation from the three-phase ($abc$) frame to the alpha-beta-zero ($\alpha\beta0$) frame is given by:
For balanced three-phase systems, the 0 component is zero, meaning all the information is contained within the two-dimensional $\alpha\beta$ plane.
What are DQ0 ($dq0$) Axes?
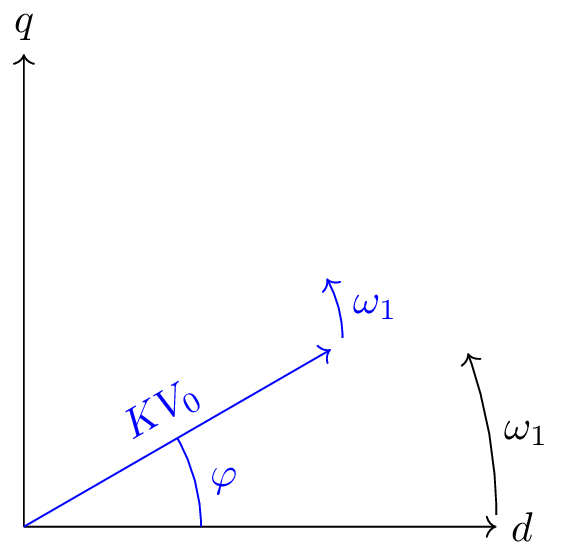
The DQ0 ($dq0$) axes form a rotating two-axis reference frame. This transformation, known as the Park transformation, takes the quantities from the stationary $\alpha\beta$ frame and rotates them at the same speed as the system's rotating magnetic field.
- The Direct ($d$) axis is typically aligned with the magnetic flux.
- The Quadrature ($q$) axis is orthogonal (90 degrees) to the direct axis.
- The zero-sequence (0) component remains the same as in the Clarke transformation.
The key advantage of the Park transformation is that for a balanced AC system, the time-varying sinusoidal quantities in the $abc$ frame become constant (DC) quantities in the $dq$ frame. This simplifies control algorithms immensely, allowing standard DC controllers like Proportional-Integral (PI) controllers to be used effectively.
Advantages and Applications of ($\alpha\beta$) and dq0 Transformations
These transformations offer significant benefits in the control and analysis of AC electrical systems:
-
Simplification of Analysis:
They reduce complex time-varying three-phase systems to simpler two-dimensional stationary ($\alpha\beta$) or DC-equivalent ($dq$) representations.
-
Decoupling of Components:
Both transformations help separate balanced components from the zero-sequence, aiding in fault detection and imbalance analysis.
-
Enhanced Control:
The $dq0$ transformation is crucial for Field-Oriented Control (FOC) of AC motors, enabling independent control of torque and flux. This leads to high-performance motor drives.
-
Computational Efficiency:
Working with fewer variables and simpler dynamics allows for more efficient control algorithms and real-time processing.
Key Applications:
-
Motor Drives:
Fundamental for advanced control of induction and synchronous motors (FOC), ensuring precise and efficient operation.
-
Power Electronics:
Widely used in control algorithms for inverters, rectifiers, and STATCOMs to simplify control structures.
-
Power System Analysis:
Aids in analyzing unbalanced conditions, fault detection, and power quality assessment.
By transforming complex three-phase variables into more manageable reference frames, the alpha-beta and DQ0 axes are indispensable tools in modern electrical engineering.
By simplifying complex three-phase variables into a more manageable two-dimensional space, the alpha-beta axes and the Clarke transformation are indispensable tools in modern electrical engineering.
Instructions:
- Use the number inputs to change the amplitude of the 3 phases.
- Use the slider to change the speed of the animation.
- Use the slider to change the phase shift between phase a and the d axis.
- Use the small slider just down here to start/stop the animation.